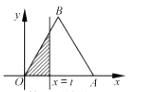
如图，在直角坐标系 xOy 中，已知点直线，将分成两部分，记左侧部分的多边形为，设各边的平方和为，各边长的倒数和为 . （Ⅰ）求分别求函数和的解析式；（Ⅱ）是否存在区间，使得函数和在该区间上均单调递减？若存在，求的最大值；若不存在，说明理由.

1. 如图，在直角坐标系 xOy 中，已知点 $\text{[math]}$ 直线 $\text{[math]}$ ，将 $\text{[math]}$ 分成两部分，记左侧部分的多边形为 $\text{[math]}$ ，设 $\text{[math]}$ 各边的平方和为 $\text{[math]}$ ， $\text{[math]}$ 各边长的倒数和为 $\text{[math]}$ .

（Ⅰ）求分别求函数 $\text{[math]}$ 和 $\text{[math]}$ 的解析式；

（Ⅱ）是否存在区间 $\text{[math]}$ ，使得函数 $\text{[math]}$ 和 $\text{[math]}$ 在该区间上均单调递减？若存在，求 $\text{[math]}$ 的最大值；若不存在，说明理由.

【考点】

分段函数的解析式求法及其图象的作法; 函数单调性的判断与证明; 分段函数的应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. ［选修4-5：不等式选讲］

已知函数 $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 的最小值；

(2) 若 $\text{[math]}$ 恒成立，求实数a的取值范围．

解答题普通

2. 已知函数 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 在给出的平面直角坐标系中画出 $\text{[math]}$ 和 $\text{[math]}$ 的图象；

(2) 若关于x的不等式 $\text{[math]}$ 恒成立，求实数a的取值范围．

解答题普通

3. 已知 $\text{[math]}$ ．

(1) 当 $\text{[math]}$ 时，求 $\text{[math]}$ 最大值；

(2) 当 $\text{[math]}$ 时，证明： $\text{[math]}$ 的解集非空．

解答题普通