1.
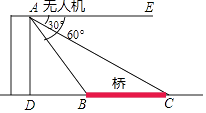
如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为 , 测得底部点B的俯角为
, 测得底部点B的俯角为 , 点A与楼
, 点A与楼 的水平距离
的水平距离 , 求这栋楼的高度
, 求这栋楼的高度 (结果保留根号).
(结果保留根号).

【考点】
解直角三角形的实际应用﹣仰角俯角问题;


 , 在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
, 在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).