1.
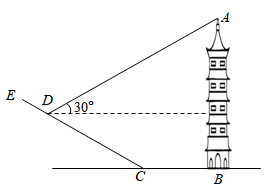
如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为300 , 沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为600 .已知坡面CD=10米,山坡的坡度 (坡度 是指坡面的铅直高度与水平宽度的比),
(坡度 是指坡面的铅直高度与水平宽度的比),
(1)求点D离地面高度(即点D到直线BC的距离);
(2)求楼房AB高度.(结果保留根式)

【考点】
解直角三角形的实际应用﹣坡度坡角问题;
解直角三角形的实际应用﹣仰角俯角问题;