1.
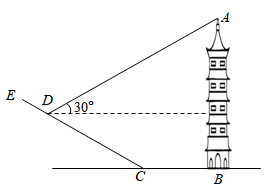
如图，小乐和小静一起从点
出发去拍摄木棉树
． 小乐沿着水平面步行17m到达点
时拍到树顶点
， 仰角为
；小静沿着坡度
的斜坡步行13m到达点C时拍到树顶点F，仰角为
， 那么这棵木棉树的高度约（ ）m．（结果精确到1m）（参考数据：
， 
， 
）
A.
22
B.
21
C.
20
D.
19
【考点】
解直角三角形的实际应用﹣坡度坡角问题;
解直角三角形的实际应用﹣仰角俯角问题;
