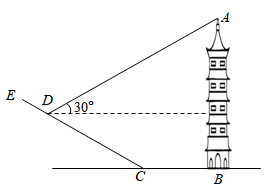
某中学依山而建，校门A处有一坡角的斜坡，长度为20米，在坡顶B处测得教学楼的楼顶C的仰角，离B点4米远的E处有一个花台，在E处测得C的仰角，的延长线交水平线于点D，求的长（结果保留根号）．

1. 某中学依山而建，校门A处有一坡角 $\text{[math]}$ 的斜坡 $\text{[math]}$ ，长度为20米，在坡顶B处测得教学楼 $\text{[math]}$ 的楼顶C的仰角 $\text{[math]}$ ，离B点4米远的E处有一个花台，在E处测得C的仰角 $\text{[math]}$ ， $\text{[math]}$ 的延长线交水平线 $\text{[math]}$ 于点D，求 $\text{[math]}$ 的长（结果保留根号）．

【考点】

解直角三角形的实际应用﹣坡度坡角问题; 解直角三角形的实际应用﹣仰角俯角问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 某天小明和同学想利用所学知识测量建筑物DE的高度，在与 $\text{[math]}$ 底端同一水平位置的点A处测得建筑物顶端D的仰角 $\text{[math]}$ 为45°，沿坡度 $\text{[math]}$ 的斜坡 $\text{[math]}$ 向上走 $\text{[math]}$ 米，到达坡顶C处，在C处测得建筑物顶端D的仰角 $\text{[math]}$ 为 $\text{[math]}$ ，若点A、B、E在同一水平线上，求建筑物 $\text{[math]}$ 的高度（结果保留整数，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

解答题容易

2. 热气球的探测器显示，从热气球A看一栋楼顶部B的仰角α为45°，看这栋楼底部C的俯角β为60°，热气球与楼的水平距离为100m，求这栋楼的高度（结果保留根号）．

解答题容易

3. 某体育看台侧面的示意图如图所示，观众区 $\text{[math]}$ 的坡度 $\text{[math]}$ 为 $\text{[math]}$ ，顶端 $\text{[math]}$ 离水平地面 $\text{[math]}$ 的高度为10m，从顶棚的 $\text{[math]}$ 处看 $\text{[math]}$ 处的仰角 $\text{[math]}$ ，竖直的立杆上 $\text{[math]}$ 、 $\text{[math]}$ 两点间的距离为 $\text{[math]}$ 处到观众区底端 $\text{[math]}$ 处的水平距离 $\text{[math]}$ 为3m，求：顶棚的 $\text{[math]}$ 处离地面的高度 $\text{[math]}$ ．（ $\text{[math]}$ ，结果精确到0.1m）

综合题容易