1.
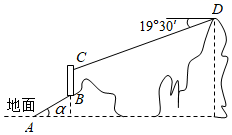
如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比)i=1∶2.4,则信号塔AB的高度约为( )(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)

A.
23米
B.
24米
C.
24.5米
D.
25米
【考点】
解直角三角形的实际应用﹣坡度坡角问题;
解直角三角形的实际应用﹣仰角俯角问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练