1.
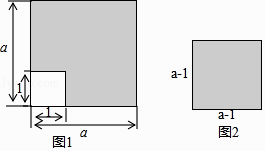
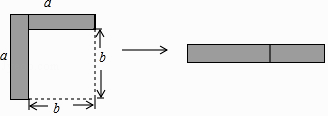
如图,将大正方形通过剪、割、拼后分解成新的图形,利用等面积法可证明某些乘法公式,在给出的4幅拼法中,其中能够验证平方差公式的有 (填序号,多选).

【考点】
平方差公式的几何背景;
基础巩固
能力提升
变式训练
拓展培优
真题演练