1.
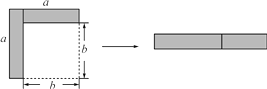
如图  ,将边长为
,将边长为  的大正方形剪去一个边长为
的大正方形剪去一个边长为  的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图
的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图  所示长方形.这两个图能解释下列哪个等式( )
所示长方形.这两个图能解释下列哪个等式( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
列式表示数量关系;
平方差公式的几何背景;
基础巩固
能力提升
变式训练
拓展培优