1.
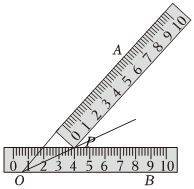
如图,一把直尺压住射线 , 另一把完全一样的直尺压住射线
, 另一把完全一样的直尺压住射线 并且与第一把直尺交于点P,小明说:“射线
并且与第一把直尺交于点P,小明说:“射线 就是
就是 的平分线.”他这样做的依据是( )
的平分线.”他这样做的依据是( )

A.
角平分线上的点到这个角两边的距离相等
B.
角的内部到角的两边距离相等的点在角的平分线上
C.
三角形三条角平分线的交点到三条边的距离相等
D.
以上均不正确
【考点】
角平分线的判定;