1.
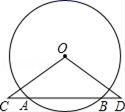
如图，AB是⊙O的直径，P为AB上一点（点P不与A、B重合），CD与EE是过点P的两条弦，且CD＝EF ， CD⊥EF ．
(1)
求证：PB平分∠FPD；
(2)
若PE＝3，PF＝5，求AB的长；
(3)
求证：当点P在AB上运动时，
的值不变，并求出这个定值．
【考点】
垂径定理;
等腰直角三角形;
角平分线的判定;
