1.
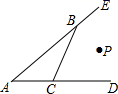
如图,点P到AE、AD、BC的距离相等,则下列说法:①点P在∠BAC的平分线上②点P在∠CBE的平分线上③点P在∠BCD的平分线上 ④点P是 ∠BAC、∠CBE、∠BCD的平分线的交点,其中正确的是( )
A.
①②③
B.
①②③④
C.
②③
D.
④
【考点】
角平分线的判定;