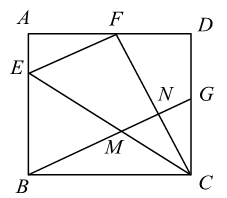
综合与探究如图，等腰直角中，，，现将该三角形放置在平面直角坐标系中，点坐标为，点坐标为.（1）过点作轴，求的长及点的坐标；（2）连接，若为坐标平面内异于点的点，且以、、为顶点的三角形与全等，请直接写出满足条件的点的坐标；（3）已知，试探究在轴上是否存在点，使是以为腰的等腰三角形？若存在，请直接写出点的坐标；若不存在，请说明理由.

1. 综合与探究

如图，等腰直角 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，现将该三角形放置在平面直角坐标系中，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 坐标为 $\text{[math]}$ .

（1）过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，求 $\text{[math]}$ 的长及点 $\text{[math]}$ 的坐标；

（2）连接 $\text{[math]}$ ，若 $\text{[math]}$ 为坐标平面内异于点 $\text{[math]}$ 的点，且以 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 全等，请直接写出满足条件的点 $\text{[math]}$ 的坐标；

（3）已知 $\text{[math]}$ ，试探究在 $\text{[math]}$ 轴上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 是以 $\text{[math]}$ 为腰的等腰三角形？若存在，请直接写出点 $\text{[math]}$ 的坐标；若不存在，请说明理由.

【考点】

轴对称的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，这两个四边形关于某直线对称，根据图形的条件求x，y.

解答题容易

2. 如图，在△ABC中，AB=AC，DE是△ABE的对称轴，△BCE的周长为14，BC=6，求AB的长.

解答题容易

1. 如图，将Rt△ABC(∠ACB=90°)纸片沿某条直线折叠，使斜边两个端点A与B重合，折痕为DE．

(1) 若AC=5cm，BC=7cm，求△ACD的周长．

(2) 若∠CAD：∠BAD=1：2，求∠B的度数．

解答题普通

2. 如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上．

(1) 图中点C的对应点是点，∠B的对应角是；

(2) 若DE＝5，BF＝2，则CF的长为；

(3) 若∠BAC＝108°，∠BAE＝30°，求∠EAF的度数．

解答题普通

3. 如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上．

(1) 图中点D的对应点是点，AE的对应边是；

(2) 若∠DAE=108°，∠EAF=39°，求∠DAC的度数．

解答题普通

1. 如图，点P为 $\text{[math]}$ 内一点，分别作出P点关于 $\text{[math]}$ 、 $\text{[math]}$ 的对称点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于M，交 $\text{[math]}$ 于N， $\text{[math]}$ ，则 $\text{[math]}$ 的周长为．

填空题容易

2. 如图是一张蕴含着轴对称变换的蝴蝶剪纸，点A与点 $\text{[math]}$ 对称，点 $\text{[math]}$ 与点 $\text{[math]}$ 对称，将其放置在直角坐标系中，点 $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

3. 如图， $\text{[math]}$ 和 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则五边形 $\text{[math]}$ 的周长为 $\text{[math]}$ $\text{[math]}$

A. 11 B. 12 C. 13 D. 14

单选题容易

1. 如图，四边形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， E、F分别为 $\text{[math]}$ 、 $\text{[math]}$ 上的动点．

(1) 如图1，已知： $\text{[math]}$ ， $\text{[math]}$ ；则DE的长为（用a表示）

(2) 如图2，已知： $\text{[math]}$ ， $\text{[math]}$ ；求：当 $\text{[math]}$ 取得最小值时 $\text{[math]}$ 的值（用b表示）

(3) 如图3，已知：G为 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ 和 $\text{[math]}$ 的角平分线，N为线段 $\text{[math]}$ 上的动点， $\text{[math]}$ ，垂足为M， $\text{[math]}$ ， $\text{[math]}$ ，求：当 $\text{[math]}$ 取最小值时，求 $\text{[math]}$ 的值（用c，d表示）

解答题困难

2. 综合探究：

“在 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三边的长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，求这个三角形的面积”．

小明同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点 $\text{[math]}$ （即 $\text{[math]}$ 三个顶点都在小正方形的顶点处），如图1所示，这样不需求 $\text{[math]}$ 的高，而借用网格就能计算出它的面积．我们把上述求 $\text{[math]}$ 面积的方法叫做构图法．