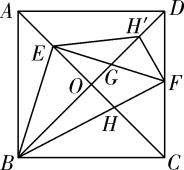
如图，在边长为2的正方形中，点E，F分别为边上的动点（不与端点重合），连接分别交对角线于点P，Q．点E，F在运动过程中，始终保持，连接．下列结论：①；的周长为4；③；④若过点B作，垂足为H，连接，则的最小值为（）

1. 如图，在边长为2的正方形 $\text{[math]}$ 中，点E，F分别为 $\text{[math]}$ 边上的动点（不与端点重合），连接 $\text{[math]}$ 分别交对角线 $\text{[math]}$ 于点P，Q．点E，F在运动过程中，始终保持 $\text{[math]}$ ，连接 $\text{[math]}$ ．下列结论：① $\text{[math]}$ ； $\text{[math]}$ 的周长为4；③ $\text{[math]}$ ；④若过点B作 $\text{[math]}$ ，垂足为H，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为 $\text{[math]}$ （）

A. ①②③ B. ①②④ C. ②③④ D. ①②③④

【考点】

三角形全等及其性质; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 汉代数学家赵爽为了证明勾股定理，创制了一幅“赵爽弦图”．如图是由弦图变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形 $\text{[math]}$ 、正方形 $\text{[math]}$ 、正方形 $\text{[math]}$ 的面积分别为 $\text{[math]}$ . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A. 567 B. 666 C. 777 D. 675

单选题容易

2. 如图，正方形 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的边长分别为2、4、6、4，四个正方形按照如图所示的方式摆放，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别位于正方形 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 对角线的交点，则阴影部分的面积和为（　　）

A. 12 B. 13 C. 14 D. 18

单选题容易

3. 如图，四边形 $\text{[math]}$ 是正方形，直线a，b，c分别通过A、D、C三点，且 $\text{[math]}$ ．若a与b之间的高是3，b与c之间的距离是5，则正方形 $\text{[math]}$ 的面积是（　　　）

A. 16 B. 30 C. 34 D. 64

单选题容易