1.
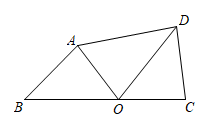
如图,正方形 的边
的边 ,
,  在坐标轴上,点B的坐标为
在坐标轴上,点B的坐标为 , 点
, 点 从点A出发,以每秒1个单位长度的速度沿
从点A出发,以每秒1个单位长度的速度沿 轴向点
轴向点 运动;点
运动;点 从点
从点 同时出发,以相同的速度沿
同时出发,以相同的速度沿 轴的正方向运动,规定点
轴的正方向运动,规定点 到达点
到达点 时,点
时,点 也停止运动.连结
也停止运动.连结 , 过
, 过 点作
点作 的垂线,与过点
的垂线,与过点 平行于
平行于 轴的直线
轴的直线 相交于点D.
相交于点D. 与
与 轴交于点
轴交于点 , 连结
, 连结 . 设点P运动的时间为
. 设点P运动的时间为 .
.

(1)
 的度数为__________,点
的度数为__________,点 的坐标为__________(用t表示);
(2)
当t为何值时,
的坐标为__________(用t表示);
(2)
当t为何值时, 是以
是以 为顶点的等腰三角形.
(3)
探索
为顶点的等腰三角形.
(3)
探索 周长是否随时间t的变化而变化,若变化,说明理由,若不变,试求这个定值.
周长是否随时间t的变化而变化,若变化,说明理由,若不变,试求这个定值.
【考点】
三角形全等及其性质;
勾股定理;
正方形的性质;