1.
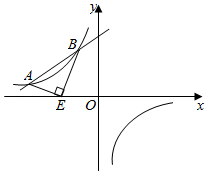
如图,直线 与抛物线
与抛物线 交于A、B两点(点A在点B的左侧),与抛物线的对称轴交于点D,抛物线与y轴交于点C
交于A、B两点(点A在点B的左侧),与抛物线的对称轴交于点D,抛物线与y轴交于点C , 抛物线的对称轴为直线
, 抛物线的对称轴为直线 .
.

(1)
求抛物线的函数表达式;
(2)
设点A、B的横坐标分别为s、t,若 , 求
, 求 的值;
(3)
设抛物线的顶点为P,当
的值;
(3)
设抛物线的顶点为P,当 时,求m的值.
时,求m的值.
【考点】
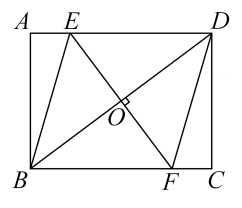
三角形全等及其性质;
勾股定理;
能力提升
真题演练