1.
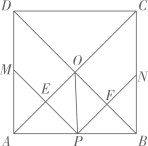
如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的两条直角边的长分别为1和3,则中间小正方形的周长是( )

A.
4
B.
8
C.
12
D.
16
【考点】
三角形全等及其性质;
正方形的性质;