1.
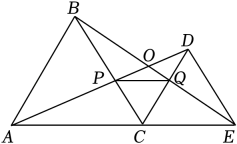
如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.

(1)求证:AD=BE;
(2)试猜想:△CGH是什么三角形,并加以证明.
【考点】
等边三角形的判定与性质;
三角形全等的判定-SAS;
三角形全等的判定-ASA;
基础巩固
能力提升
变式训练
拓展培优