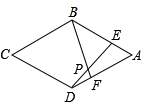
阅读材料：已知：如图1，是直角三角形，，．求证：证明：如图2，延长至点，使，连接．，．，．在和中．（全等三角形的对应边相等）．是等边三角形（有一个角等于的等腰三角形是等边三角形）．【知识运用】（1）如图1，在Rt中，，若，，则______；【类比证明】（2）如图3，请类比以上证明过程，证明：在中，若，，求证：；【迁移创新】请你尝试解决以下问题．（3）如图4，等边中，延长，，使，连接，．求证：．

1. 阅读材料：

已知：如图1， $\text{[math]}$ 是直角三角形， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$

证明：如图2，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$

在 $\text{[math]}$ 和 $\text{[math]}$ 中

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$ ．

$\text{[math]}$ $\text{[math]}$ （全等三角形的对应边相等）．

$\text{[math]}$ $\text{[math]}$ 是等边三角形（有一个角等于 $\text{[math]}$ 的等腰三角形是等边三角形）．

【知识运用】（1）如图1，在Rt $\text{[math]}$ 中， $\text{[math]}$ ，

若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ______；

【类比证明】（2）如图3，请类比以上证明过程，证明：在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；

【迁移创新】请你尝试解决以下问题．

（3）如图4，等边 $\text{[math]}$ 中，延长 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

【考点】

等边三角形的判定与性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题困难

1. 如图，E是等边三角形 $\text{[math]}$ 的边 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

解答题容易

2. 如图是燕子风筝的骨架平面图， $\text{[math]}$ $\text{[math]}$ ，求 $\text{[math]}$ 的大小．

证明题容易

3. 如图，点 $\text{[math]}$ 在 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．

证明题容易