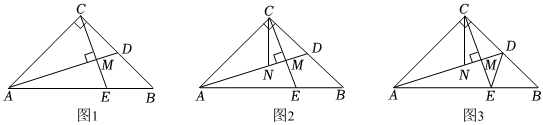
【方法探究】如下图，在中，平分，，探究，，之间的数量关系；嘉铭同学通过思考发现，可以通过“截长、补短”两种方法解决问题：方法1：如下图，在上截取，使得，连接，可以得到全等三角形，进而解决此问题方法2：如下图，延长到点，使得，连接，可以得到等腰三角形，进而解决此问题

0 返回首页

1. 【方法探究】如下图，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系；

嘉铭同学通过思考发现，可以通过“截长、补短”两种方法解决问题：

方法1：如下图，在 $\text{[math]}$ 上截取 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ，可以得到全等三角形，进而解决此问题 $\text{[math]}$

方法2：如下图，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ $\text{[math]}$ ，连接 $\text{[math]}$ ，可以得到等腰三角形，进而解决此问题 $\text{[math]}$

(1) 根据探究，直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系；

(2) 【迁移应用】

如下图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并证明．

(3) 【拓展延伸】

如下图， $\text{[math]}$ 为等边三角形，点 $\text{[math]}$ 为 $\text{[math]}$ 延长线上一动点，连接 $\text{[math]}$ ．以 $\text{[math]}$ 为边在 $\text{[math]}$ 上方作等边 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 并延长，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．若 $\text{[math]}$ ，求证： $\text{[math]}$ ；

【考点】

等边三角形的判定与性质; 三角形全等的判定-SAS; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 综合与探究：问题情景：如图 $\text{[math]}$ 所示，已知，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中线，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，且交 $\text{[math]}$ 于点 $\text{[math]}$ ．

(1) $\text{[math]}$ 探究一 $\text{[math]}$ 小虎通过度量发现 $\text{[math]}$ ，请你帮他说明理由；

(2) $\text{[math]}$ 探究二 $\text{[math]}$ 小明在图中添加了一条线段 $\text{[math]}$ ，且 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，如图 $\text{[math]}$ 所示，即可得 $\text{[math]}$ ，符合题意吗？请说明理由；

(3) $\text{[math]}$ 探究三 $\text{[math]}$ 小刚在 $\text{[math]}$ 的基础上，连接 $\text{[math]}$ ，如图 $\text{[math]}$ 所示，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积．

实践探究题困难

(1) 【初步感知】

如图1，已知 $\text{[math]}$ 为等边三角形，点 $\text{[math]}$ 为边 $\text{[math]}$ 上一动点 $\text{[math]}$ 点 $\text{[math]}$ 不与点 $\text{[math]}$ ，点 $\text{[math]}$ 重合 $\text{[math]}$ 以 $\text{[math]}$ 为边向右侧作等边 $\text{[math]}$ ，连接 $\text{[math]}$ ．

求证： $\text{[math]}$ ≌ $\text{[math]}$ ；

(2) 【类比探究】

如图 $\text{[math]}$ ，若点 $\text{[math]}$ 在边 $\text{[math]}$ 的延长线上，随着动点 $\text{[math]}$ 的运动位置不同，猜想并证明： $\text{[math]}$ 与 $\text{[math]}$ 的位置关系为：； $\text{[math]}$ 线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系为：；

(3) 【拓展应用】

如图 $\text{[math]}$ ，在等边 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是边 $\text{[math]}$ 上一定点且 $\text{[math]}$ ，若点 $\text{[math]}$ 为射线 $\text{[math]}$ 上动点，以 $\text{[math]}$ 为边向右侧作等边 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 请问： $\text{[math]}$ 是否有最小值？若有，请直接写出其最小值；若没有，请说明理由．

实践探究题普通

3. 综合与实践

如图， $\text{[math]}$ 是等边三角形， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 在线段 $\text{[math]}$ 的延长线上取点 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ，直线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ .求证： $\text{[math]}$ .

实践探究题普通