1.
综合与实践
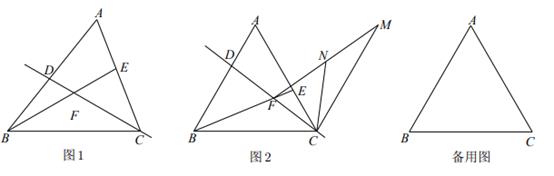
如图,是等边三角形,
,
分别是
,
的中点,连接
.

(1)
求证: ;
(2)
在线段
;
(2)
在线段 的延长线上取点
的延长线上取点 ,
,  , 使
, 使 , 直线
, 直线 ,
,  交于点
交于点 .求证:
.求证: .
.
【考点】
等边三角形的判定与性质;
三角形全等的判定-SAS;
能力提升
真题演练