1.
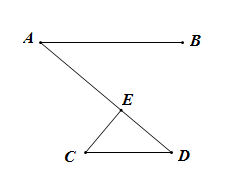
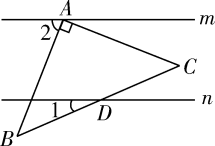
健康骑行越来越受到老百姓的喜欢,自行车(图1)的示意图如图2所示,其中

 ,
, 

 . 若
. 若 ,
,  , 求
, 求 的度数.
的度数.

【考点】
平行线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练