1.
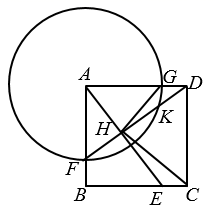
如图,在正方形ABCD中,AB=6,E为CD上一动点,AE交BD于点F,过F作FH⊥AE交BC于点H,过H作GH⊥BD于点G,连接AH,以下四个结论:① AF=FH;② ;③ FC=
;③ FC= ;④ BD=2GF,其中正确的结论有.(填序号)
;④ BD=2GF,其中正确的结论有.(填序号)

【考点】
三角形全等及其性质;
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练