1.
已知正方形 中,点E在
中,点E在 边上(不与两端点重合).
边上(不与两端点重合).

(1)
如图1,连接 , 若
, 若 平分
平分 ,
,  , 求正方形
, 求正方形 的面积;
(2)
如图2,将
的面积;
(2)
如图2,将 绕点A逆时针方向旋转
绕点A逆时针方向旋转 得到线段
得到线段 , 过点H作
, 过点H作 交
交 于点F,直线
于点F,直线 交
交 于点G,猜想线段
于点G,猜想线段 ,
,  ,
,  之间的数量关系,并说明理由;
(3)
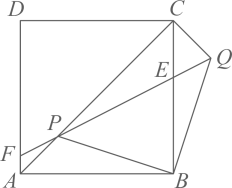
如图3,若正方形的边长是4,点P是
之间的数量关系,并说明理由;
(3)
如图3,若正方形的边长是4,点P是 边上一点,且
边上一点,且 , 连接
, 连接 ,
,  , 将
, 将 沿
沿 翻折到同一平面上的
翻折到同一平面上的 , 连接
, 连接 ,
,  , 请直接写出
, 请直接写出 的最小值.
的最小值.
【考点】
三角形全等及其性质;
正方形的性质;
相似三角形的判定与性质;
旋转的性质;