1.
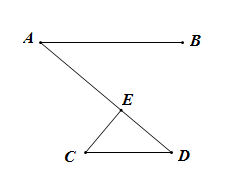
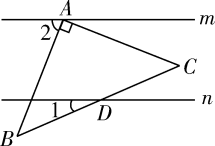
某城市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中 都与地面
都与地面 平行,其中
平行,其中 ,
,  . 若
. 若 与
与 平行,求
平行,求 的度数.
的度数.

【考点】
平行线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练