1.
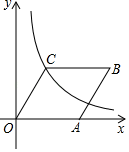
《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几?”
译文:“秋千静止的时候,踏板离地1尺,将它往前推送两步(两步10尺)时,此时踏板升高离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”

若设秋千绳索长为x尺,则可列方程为( ).
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
勾股定理;