1.

(1)
【基础巩固】
(2)
【尝试应用】
(3)
【拓展提高】
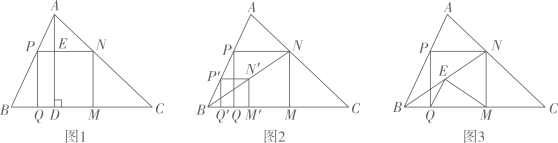
如图1,在中,点D是
上的一点,且
, 求证:
.
如图2,在(1)的条件下,过点D作 , 交
于点E . 若
,
, 求
的长.
如图3,在中,点E是
的中点,连结
交
于点F , 且
. 若
, 求
的值.
【考点】
相似三角形的判定与性质;
相似三角形的应用;
能力提升
真题演练