1.
小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)
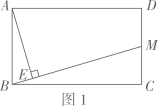
温故:如图1,在△  中,
中,  ⊥
⊥  于点
于点  ,正方形
,正方形  的边
的边  在
在  上,顶点
上,顶点  ,
,  分别在
分别在  ,
,  上,若
上,若  ,
,  ,求正方形
,求正方形  的边长.
(2)
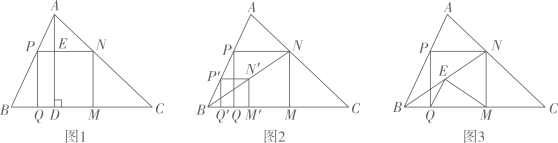
操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△
的边长.
(2)
操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△  ,在
,在  上任取一点
上任取一点  ,画正方形
,画正方形  ,使
,使  ,
,  在
在  边上,
边上,  在△
在△  内,连结
内,连结  并延长交
并延长交  于点N,画
于点N,画  ⊥
⊥  于点
于点  ,
,  ⊥
⊥  交
交  于点
于点  ,
,  ⊥
⊥  于点
于点  ,得到四边形P
,得到四边形P  .小波把线段
.小波把线段  称为“波利亚线”.
(3)
拓展:在(2)的条件下,于波利亚线
称为“波利亚线”.
(3)
拓展:在(2)的条件下,于波利亚线  上截取
上截取  ,连结
,连结  ,
,  (如图3).当
(如图3).当  时,猜想∠
时,猜想∠  的度数,并尝试证明.
的度数,并尝试证明.
推理:证明图2中的四边形 是正方形.
【考点】
矩形的性质;
相似三角形的判定与性质;
相似三角形的应用;
能力提升