1.
(1)
【问题情境 建构函数】
(2)
【由数想形 新知初探】
(3)
【数形结合 深度探究】
(4)
【抽象回归 扩展总结】
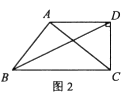
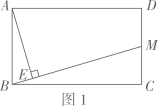
如图1,在矩形中,
是
的中点,
, 垂足为
.设
, 试用含
的代数式表示
.
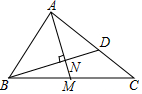
在上述表达式中,与
成函数关系,其图像如图2所示.若
取任意实数,此时的函数图象是否具有对称性?若有,请说明理由,并在图2上补全函数图象.

在“取任意实数”的条件下,对上述函数继续探究,得出以下结论:①函数值
随
的增大而增大;②函数值
的取值范围是
;③存在一条直线与该函数图象有四个交点;④在图像上存在四点
, 使得四边形
是平行四边形.其中正确的是.(写出所有正确结论的序号)
若将(1)中的“AB=4”改成“”,此时
关于
的函数表达式是 .一般地,当
取任意实数时,类比一次函数、反比例函数、二次函数的研究过程,探究此类函数的相关性质(直接写出3条即可).
【考点】
矩形的性质;
相似三角形的判定与性质;