0 返回首页
1. 定义：如果四边形的一条对角线把该四边形分割成两个等腰三角形，且这条对角线是这两个等腰三角形的腰，那么我们称这个四边形为“双等腰四边形”。

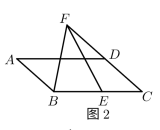
(1) 如图①，在四边形ABCD中，∠BAD=∠BCD=90°，连结BD，E是BD的中点，连结AE，CE.

①试判断四边形ABCE是否为“双等腰四边形”，并说明理由.

②若∠AEC=90°，求∠ABC的度数.
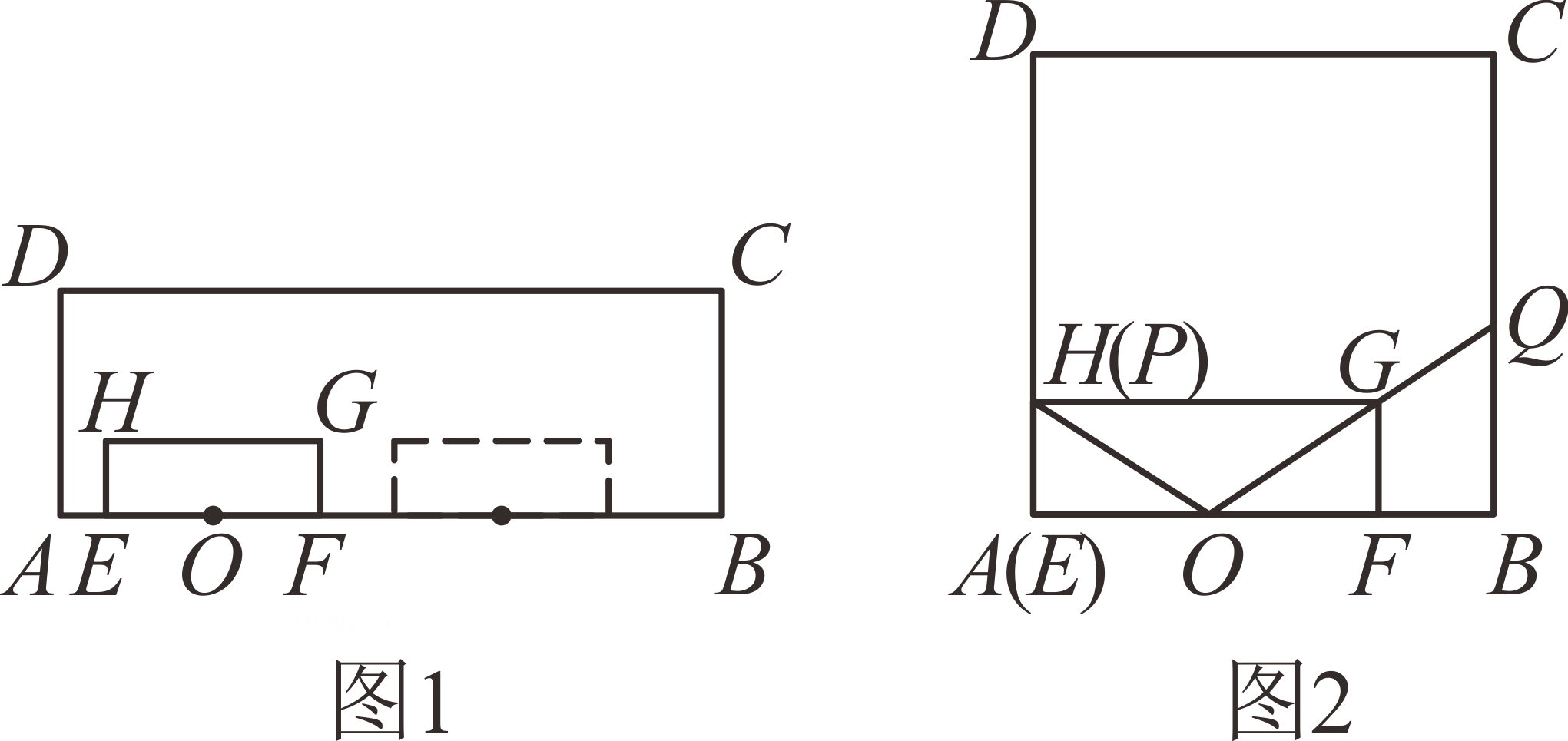
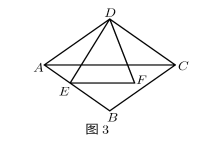
(2) 如图②，E是矩形ABCD内一点，F是边CD上一点，四边形AEFD是“双等腰四边形”，且AD=DE.延长AE交BC于点G，连结FG.若AD=5，求AB的长。
【考点】
相似三角形的判定与性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
实践探究题 困难
能力提升
真题演练
换一批
1. 如图1，小丽借助几何软件进行数学探究：第一步，画出矩形ABCD和矩形EFGH，点E，F在边AB上 ， 且点C，D，G，H在直线AB的同侧；第二步，设置 ， 矩形EFGH能在边AB上左右滑动；第三步，画出边EF的中点 ， 射线OH与射线AD相交于点（点 ， 不重合），射线OG与射线BC相交于点（点Q，C不重合），观测DP，CQ的长度.

(1) 如图2，小丽取AB=4，EF=3，m=1，n=3，滑动矩形EFGH，当点E，A重合时，CQ=.
(2) 小丽滑动矩形EFGH，使得О恰为边AB的中点.她发现对于任意的m≠n，DP=CQ总成立.请说明理由.
(3) 经过数次操作，小丽猜想，设定m，n的某种数量关系后，滑动矩形EFGH，DP=CQ总成立.小丽的猜想是否正确？请说明理由.
实践探究题 困难
2.
(1) 问题背景：如图1，点E在BC上，AB⊥BC，AE⊥ED，DC⊥BC，求证：＝ ．
(2) 尝试应用：如图2，在▱ABCD中，点F在DC边上，将△ADF沿AF折叠得到△AEF，且点E恰好为BC边的中点，求的值．
(3) 拓展创新：如图3，在菱形ABCD中，点E，F分别在BC，DC边上，∠AFE＝∠D，AE⊥FE，FC＝2．EC＝6．请直接写出cos∠AFE的值．
实践探究题 困难
3. 【基础巩固】
(1) 如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．
(2) 【尝试应用】

如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF＝4，BE＝3，求AD的长．
(3) 【拓展提高】

如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，∠EDF＝∠BAD，AE＝2，DF＝5，求菱形ABCD的边长．

 
实践探究题 困难