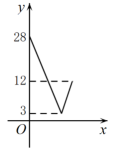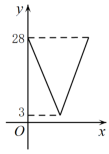1.
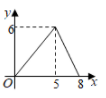
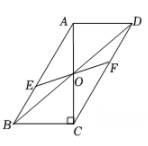
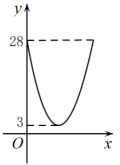
如图,在正方形ABCD中,AB=4,动点M,N 分别从点A,B同时出发,沿射线AB,射线BC的方向匀速运动,且速度的大小相等,连结DM,MN,ND.设点M运动的路程为x(0≤x≤4),△DMN的面积为S,下列图象中能反映S关于x的函数关系的是( )

A.
 B.
B.
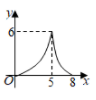
 C.
C.
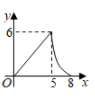
 D.
D.

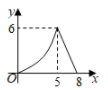
 B.
B.
 C.
C.
 D.
D.

【考点】
二次函数的实际应用-几何问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练