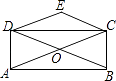
如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD.若AC=10，则四边形OCED的周长是.

菱形的定义	有一组的平行四边形叫做菱形.
菱形的性质	1.菱形具有平行四边形所有的性质.
	2.菱形的四条边相等，对角线互相，并且每条对角线平分一组对角.
	3.菱形既是一个轴对称图形，两条对角线所在的直线就是它的对称轴，又是中心对称图形，它的对称中心就是对角线的交点.
	4.菱形的面积等于对角线乘积的一半.
菱形的判定	1.定义法.
	2.四条边的四边形是菱形.
	3.对角线的平行四边形是菱形.

基础知识填空容易

填空题容易

对称性： ①矩形是一个轴对称图形，它至少有条对称轴．

②矩形是中心对称图形，它的对称中心是的交点．

定理： ①矩形的四个角都是直角．

②矩形的对角线互相平分且相等．
（3）判定：

①定义法．

②有三个角是直角的四边形是矩形．

③对角线相等的平行四边形是矩形．

④对角线相等且互相平分的四边形是矩形．

（4）拓展： ①矩形的两条对角线把矩形分成四个面积相等的等腰三角形．

②矩形的面积等于两邻边的积．

基础知识填空容易

填空题普通

填空题普通

填空题普通

单选题普通

单选题普通

单选题容易

1. 如图，四边形 $\text{[math]}$ 是矩形， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 上的点， $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ．