1.
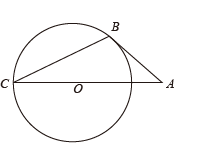
已知：如图所示，在△OAB中，OA=OB，⊙O与AB相切于点C．求证：AC=BC．小明同学的证明过程如下框：
证明：连结OC，
∵OA=OB，
∴∠A=∠B．
又∵OC=OC，
∴△OAC≌△OBC，
∴AC=BC．
小明的证法是否正确？若正确，请在框内打“√”；若错误，请写出你的证明过程．
【考点】
等腰三角形的性质;
切线的性质;
