1.
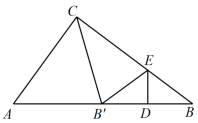
如图,在3×3的正方形网格中,每个小正方形边长为1,点A,B,C,D均为格点,以A为圆心,AB长为半径作弧,交网格线CD于点E,则C,E两点间的距离为( )

A.
 B.
3-
B.
3- C.
C.
 D.
D.
 -
-
【考点】
勾股定理;
线段的和、差、倍、分的简单计算;
基础巩固
能力提升
变式训练
拓展培优
真题演练