1.
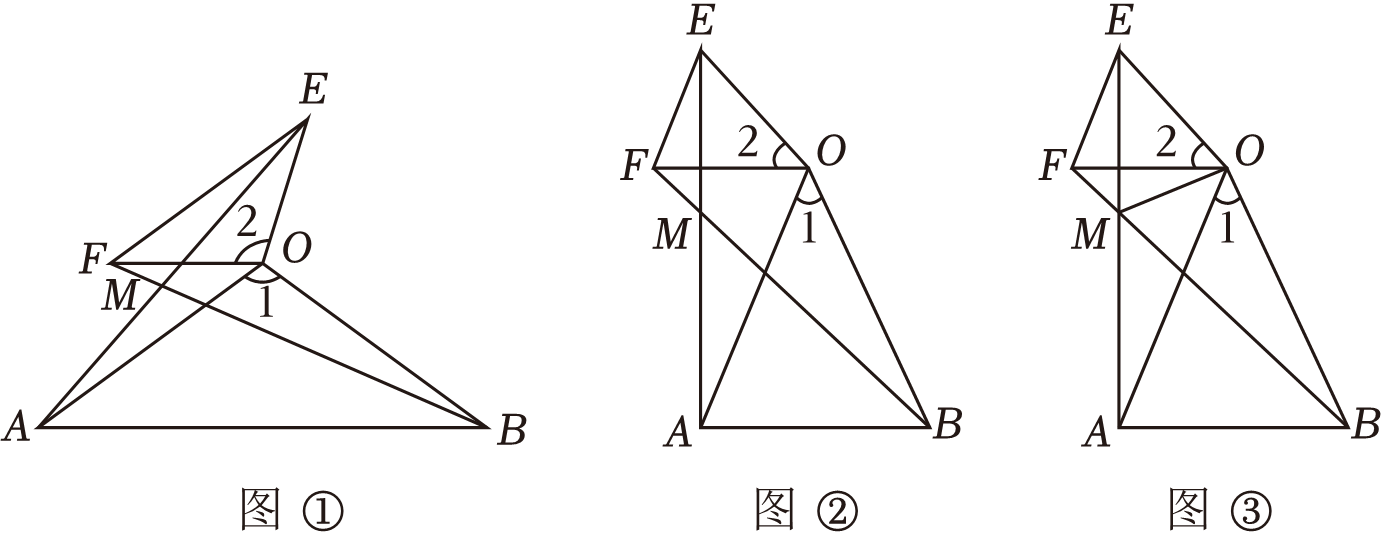
如图,在△OAB和△OCD中,OA=OB , OC=OD,OA>OC , ∠AOB=∠COD=40°,连接AC,BD交于点M , 连接OM . 下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC . 其中正确的个数为( )

A.
4
B.
3
C.
2
D.
1
【考点】
角平分线的判定;
三角形全等的判定-SAS;
三角形全等的判定-AAS;