1.
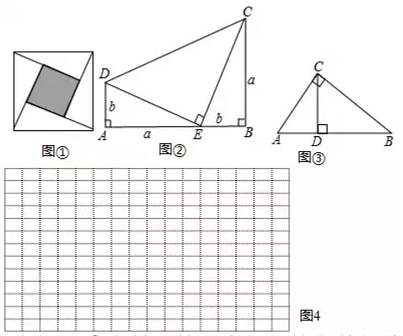
在学习勾股定理时，甲同学用四个相同的直角三角形
直角边长分别为
， 
， 斜边长为
构成如图所示的正方形；乙同学用边长分别为 ， 的两个正方形和长为 ， 宽为的两个长方形构成如图所示的正方形，甲、乙两位同学给出的构图方案，可以证明勾股定理的是（ ）
A.
甲
B.
乙
C.
甲，乙都可以
D.
甲，乙都不可以
【考点】
完全平方公式的几何背景;
勾股定理的证明;
