1.
教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为 
，较小的直角边长都为 
，斜边长都为 
），大正方形的面积可以表示为 
，也可以表示为 
，由此推导出重要的勾股定理：如果直角三角形两条直角边长为 
，斜边长为 ，则 
．
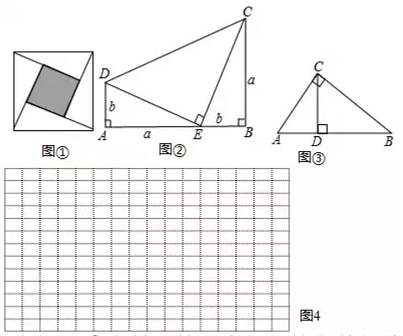
(1)
图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．
(2)
如图③，在 
中， 
是 
边上的高， 
， 
， 
，设 
，求 
的值．
(3)
试构造一个图形，使它的面积能够解释 
，画在如图4的网格中，并标出字母 
所表示的线段．
【考点】
完全平方公式的几何背景;
勾股定理;
勾股定理的证明;
能力提升
