1.
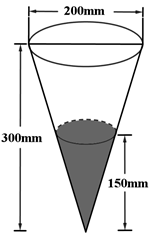
某班级到一工厂参加社会实践劳动,加工出如图所示的圆台 , 在轴截面ABCD中,
, 在轴截面ABCD中, , 且
, 且 , 下列说法正确的是( )
, 下列说法正确的是( )

A.
该圆台轴截 面面积为
面面积为 B.
该圆台的体积为
B.
该圆台的体积为 C.
该圆台的表面积为
C.
该圆台的表面积为 D.
沿着该圆台表面,从点
D.
沿着该圆台表面,从点 到
到 中点的最短距离为
中点的最短距离为
【考点】
旋转体(圆柱/圆锥/圆台/球)的结构特征;
基础巩固
能力提升
变式训练
拓展培优
真题演练