1.
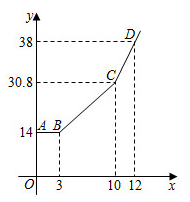
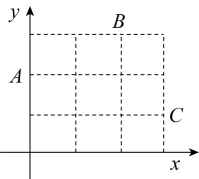
在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算
. 分别计算 ,
,  的值,其中最大的值等于.
的值,其中最大的值等于.
【考点】
待定系数法求一次函数解析式;
基础巩固
能力提升
变式训练
拓展培优
真题演练