1.
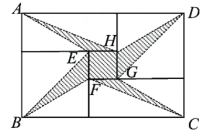
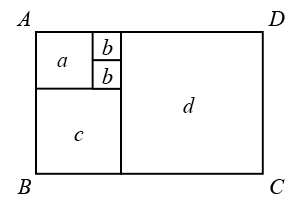
如图,将长方形 的各边向外作正方形,若四个正方形周长之和为56,面积之和为58,则长方形
的各边向外作正方形,若四个正方形周长之和为56,面积之和为58,则长方形 的面积为.
的面积为.

【考点】
矩形的性质;
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练