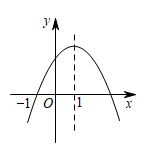1.
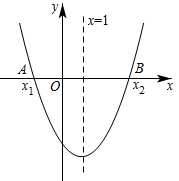
已知二次函数 , 当
, 当 时,该函数取最大值12.设该函数图象与x轴的一个交点的横坐标为
时,该函数取最大值12.设该函数图象与x轴的一个交点的横坐标为 , 若
, 若 , 则a的取值范围是.
, 则a的取值范围是.
【考点】
二次函数图象与系数的关系;
二次函数的最值;
二次函数图象与坐标轴的交点问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练