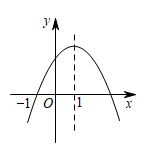1.
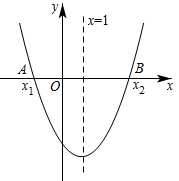
如图1,在平面直角坐标系  中,已知抛物线
中,已知抛物线  :
:  (
(  ).
).

(1)
若抛物线过点  ,求出抛物线的解析式;
(2)
当
,求出抛物线的解析式;
(2)
当  时,
时,  的最小值是
的最小值是  ,求
,求  时,
时,  的最大值;
(3)
已知直线
的最大值;
(3)
已知直线  与抛物线
与抛物线  (
(  )存在两个交点,若两交点到
)存在两个交点,若两交点到  轴的距离相等,求
轴的距离相等,求  的值;
(4)
如图2,作与抛物线
的值;
(4)
如图2,作与抛物线  关于
关于  轴对称且对称轴相同的抛物线
轴对称且对称轴相同的抛物线  ,当抛物线
,当抛物线  与抛物线
与抛物线  围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出
围成的封闭区域内(不包括边界)共有11个横、纵坐标均为整数的点时,直接写出  的取值范围.
的取值范围.
【考点】
二次函数图象与系数的关系;
二次函数的最值;
二次函数图象与坐标轴的交点问题;