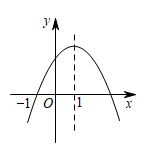1.
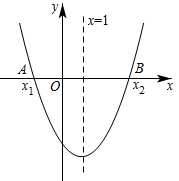
二次函数 与
与 轴的两个交点横坐标
轴的两个交点横坐标 ,
,  满足
满足 . 当
. 当 时,该函数有最大值
时,该函数有最大值 , 则
, 则 的值为( )
的值为( )
A.
-4
B.
-2
C.
1
D.
2
【考点】
二次函数的最值;
二次函数图象与坐标轴的交点问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练