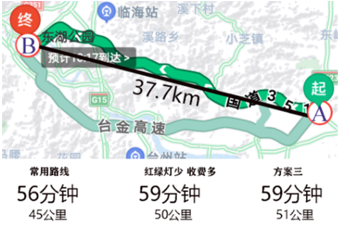
1.
如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
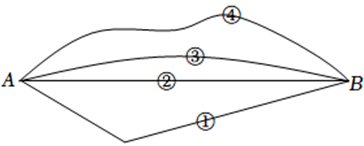

A.
①
B.
②
C.
③
D.
④
【考点】
两点之间线段最短;
基础巩固
能力提升
变式训练
拓展培优
真题演练