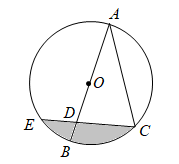
如图，在Rt△ABC中，，，，将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为（）

1. 如图，在Rt△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点B顺时针旋转90°得到 $\text{[math]}$ .在此旋转过程中 $\text{[math]}$ 所扫过的面积为（）

A. 25π+24 B. 5π+24 C. 25π D. 5π

【考点】

三角形的面积; 勾股定理; 扇形面积的计算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 一个扇形的半径为6，圆心角为120°，则该扇形的面积是（）

A. 2π B. 4π C. 12π D. 24π

单选题容易

2. 在直角三角形中，若勾为3，股为4，则弦为（）

A. 5 B. 6 C. 7 D. 8

单选题容易

3. 已知一个扇形的圆心角为 $\text{[math]}$ ，半径是6，则这个扇形的面积是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易