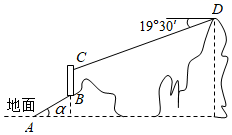
某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼的高度．如图所示，其中观景平台斜坡的长是20米，坡角为，斜坡底部与大楼底端的距离为74米，与地面垂直的路灯的高度是3米，从楼顶测得路灯项端处的俯角是．试求大楼的高度．（参考数据：，，，，，）

1. 某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼 $\text{[math]}$ 的高度．如图所示，其中观景平台斜坡 $\text{[math]}$ 的长是20米，坡角为 $\text{[math]}$ ，斜坡 $\text{[math]}$ 底部 $\text{[math]}$ 与大楼底端 $\text{[math]}$ 的距离 $\text{[math]}$ 为74米，与地面 $\text{[math]}$ 垂直的路灯 $\text{[math]}$ 的高度是3米，从楼顶 $\text{[math]}$ 测得路灯 $\text{[math]}$ 项端 $\text{[math]}$ 处的俯角是 $\text{[math]}$ ．试求大楼 $\text{[math]}$ 的高度．

（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

【考点】

解直角三角形的实际应用﹣坡度坡角问题; 解直角三角形的实际应用﹣仰角俯角问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 河南省洛阳市应天门是隋唐洛阳城·宫城——紫微城的正南门，俗称五凤楼．应天门是一座由门楼、朵楼和东西阙楼及其间的廊庑为一体的“凹”字形巨大建筑群，两侧的阙高的高度相同，被称为“天下第一门”．某校数学兴趣小组要测量应天门两侧的阙高的高度，如图，他们在点 $\text{[math]}$ 处测得应天门两侧的阙的最高点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，再往应天门两侧阙高方向前进 $\text{[math]}$ 至点 $\text{[math]}$ 处，测得应天门两侧阙的最高点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，根据这个兴趣小组测得的数据，计算应天门两侧阙高 $\text{[math]}$ 的高度．（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

计算题容易

2. 如图，无人机在塔树上方 $\text{[math]}$ 处悬停，测得塔顶 $\text{[math]}$ 的俯角为 $\text{[math]}$ ，树高 $\text{[math]}$ 为 $\text{[math]}$ 米，无人机竖直高度 $\text{[math]}$ 为 $\text{[math]}$ 米，且 $\text{[math]}$ 点到塔底 $\text{[math]}$ 的距离比到树底 $\text{[math]}$ 的距离多 $\text{[math]}$ 米，求塔高 $\text{[math]}$ 的值．（参考数据： $\text{[math]}$ ）

解答题容易

3. 如图，建筑物AB垂直于地面，测角机器人先在C处测得A的仰角为 $\text{[math]}$ ，再向着B前进6米到D处，测得A的仰角为 $\text{[math]}$ ．求建筑物AB的高度（结果精确到米）．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

解答题容易