1.
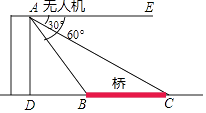
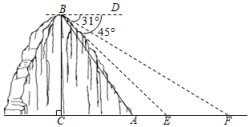
某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,河旁有一座小山,山高 , 点C、A与河岸E、F在同一水平线上,从山顶B处测得河岸E和对岸F的俯角分别为
, 点C、A与河岸E、F在同一水平线上,从山顶B处测得河岸E和对岸F的俯角分别为 ,
,  . 若在此处建桥,求河宽
. 若在此处建桥,求河宽 的长.(结果精确到
的长.(结果精确到 )[参考数据:
)[参考数据: ,
,  ,
, 

【考点】
解直角三角形的实际应用﹣仰角俯角问题;