1.
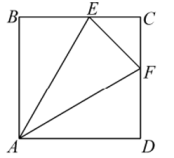
正方形ABCD的边长是8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB交AM于点N,当PB=AM时,PN的长是 .
【考点】
直角三角形全等的判定-HL;
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练