1.
推理填空:
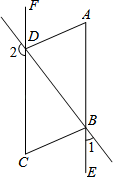
如图, 于D,
于G,
,可得
平分
.
理由如下:∵ 于D,
于G,(已知)
∴ ,( ▲ )
∴ ,( ▲ )
∴ ▲ , ( ▲ )
,( ▲ )
又∵ ,( ▲ )
∴ ▲ , ( ▲ )
∴ 平分
.( ▲ )

【考点】
推理与论证;


 三角形内角和定理:三角形三个内角和等于180°,
三角形内角和定理:三角形三个内角和等于180°,
