1.
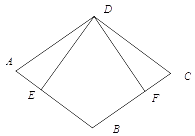
如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21 cm,CA=15cm,求菱形AMNP的周长.

【考点】
菱形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练