1.
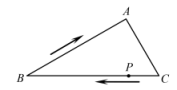
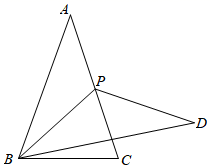
如图  中,
中,  ,
,  ,点
,点  从
从  处向
处向  处运动,每秒
处运动,每秒  ,点
,点  从
从  处向
处向  处运动,每秒
处运动,每秒  ,其中一个动点到达端点后,另一个点停止运动.当
,其中一个动点到达端点后,另一个点停止运动.当  时,运动时间为( )
时,运动时间为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
三角形-动点问题;
能力提升
变式训练
拓展培优
真题演练